Next: SCF Control and Stabilization Up: Electronic State Control Previous: Keyword SMEAR Contents
|
MAX= | Maximum number of SCF cycles for which the configuration is used. By default it is used for all SCF cycles. | ||
| OCCUPY | The (fractional) occupation of the specified atomic configuration is given explicitly in the subsequent input. |
| (9) |
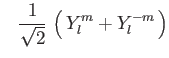 |
(10) | ||
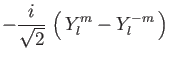 |
(11) |
The ordering of the integer numbers in the configuration line follows the
![]() (shell) and
(shell) and ![]() index of the real spherical harmonics:
index of the real spherical harmonics:
| Shell | | | | | ||||||||||
|
| 0 | | | | ||||||||||
|
| 0 | -1 | 0 | 1 | -2 | -1 | 0 | 1 | 2 | | ||||
| Orbital | | | | |
| | |
| | |
As an example the open-shell (OKS or ROKS) triplet ground state
configuration of the carbon atom,
![]() , can be defined in
the keyword block of CONFIGURE as:
, can be defined in
the keyword block of CONFIGURE as:
2 1 1 0 2 0 0 0
The first line defines the ![]() -orbital configuration with two
electrons in the most stable
-orbital configuration with two
electrons in the most stable ![]() -orbitals (
-orbitals (![]() and
and ![]() ) and one electron each
in the most stable
) and one electron each
in the most stable ![]() (
(![]() ) and
) and ![]() (
(![]() )
) ![]() -orbital (
-orbital (![]() and
and ![]() ). The second line assigns two electrons to the two most stable
). The second line assigns two electrons to the two most stable ![]()
![]() -orbitals. Unspecified shells (here
-orbitals. Unspecified shells (here ![]() and higher) are not considered. If
Cartesian orbitals are used, only the number of electrons in the
and higher) are not considered. If
Cartesian orbitals are used, only the number of electrons in the ![]() ,
, ![]() ,
, ![]() ,
etc. shells needs to be specified. Thus, for Cartesian orbitals the foregoing
configuration definition changes to:
,
etc. shells needs to be specified. Thus, for Cartesian orbitals the foregoing
configuration definition changes to:
2 2 2 0
Because of the ![]() -orbital degeneracy, the chosen Cartesian
configuration has to be stabilized during the SCF procedure (see 4.4.5
or 4.5.7). The calculation of the triplet carbon ground state with
spherical and Cartesian orbitals using CONFIGURE is described by the
examples
-orbital degeneracy, the chosen Cartesian
configuration has to be stabilized during the SCF procedure (see 4.4.5
or 4.5.7). The calculation of the triplet carbon ground state with
spherical and Cartesian orbitals using CONFIGURE is described by the
examples ![[*]](crossref.png) and
and ![[*]](crossref.png) in the deMon2k Tutorial, respectively.
in the deMon2k Tutorial, respectively.
To access excited atomic states or to use fractional occupation
numbers, the option OCCUPY must be used. In this case, an explicit
definition of the orbital occupation is expected after the orbital
configuration line(s). In the case of spherical atomic orbitals an input
line describing the occupation of each real spherical harmonic orbital
type is needed. The occupation numbers can be given as real or integer
values. To describe the excited triplet state of carbon,
![]() , for example, the following keyword
body of CONFIGURE, using the option OCCUPY, is needed.
, for example, the following keyword
body of CONFIGURE, using the option OCCUPY, is needed.
3 1 1 0 2 0 0 0 1 0 1 1 1 1 1
Here, the 3 in the first configuration line indicates that the
three lowest ![]() -type
-type ![]() -orbitals will be occupied (note that this number does not represent the number of electrons in these orbitals). The 1 1 0 in
the first line indicates that the
-orbitals will be occupied (note that this number does not represent the number of electrons in these orbitals). The 1 1 0 in
the first line indicates that the ![]() and
and ![]()
![]() -orbitals will
be occupied (we assume the default spherical orbitals with the order given above).
The second line gives the
-orbitals will
be occupied (we assume the default spherical orbitals with the order given above).
The second line gives the ![]() configuration. Here, only
the two lowest
configuration. Here, only
the two lowest ![]()
![]() orbitals will be occupied. Occupation patterns begin
in the third line, which, for the three lowest
orbitals will be occupied. Occupation patterns begin
in the third line, which, for the three lowest ![]() -type
-type ![]() orbitals in
this example is (
orbitals in
this example is ( 1 0 1 ). This scheme has the lowest ![]()
![]() -orbital
occupied with 1 electron, the next one empty, and the third one again occupied
with 1 electron. Therefore, a hole in the
-orbital
occupied with 1 electron, the next one empty, and the third one again occupied
with 1 electron. Therefore, a hole in the ![]()
![]() -orbital occupation is produced.
The next two occupation lines assign 1 electron to the
-orbital occupation is produced.
The next two occupation lines assign 1 electron to the ![]() and 1 to the
and 1 to the ![]()
![]() -orbital. The last occupation has the two lowest
-orbital. The last occupation has the two lowest ![]()
![]() -orbitals occupied
with 1 electron each. Please also note that zero (0) entries in the configuration
line(s) do not have corresponding occupation lines. Example
-orbitals occupied
with 1 electron each. Please also note that zero (0) entries in the configuration
line(s) do not have corresponding occupation lines. Example ![[*]](crossref.png) on page
on page
![[*]](crossref.png) of the deMon2k Tutorial describes the calculation of the excited
of the deMon2k Tutorial describes the calculation of the excited
![]() carbon triplet state.
carbon triplet state.
As already mentioned, the OCCUPY option may also be used to generate fractional occupations, e.g. for the calculation of spherical atoms. In the case of the triplet carbon ground state, the following CONFIGURE keyword body produces a spherical atom.
2 1 1 1 2 0 0 0 1 1 0.6666 0.6666 0.6666 1 1
The first configuration line describes the occupation of two
![]()
![]() -orbitals and of all three
-orbitals and of all three ![]() -orbitals. According to the
specified occupation (third line), the two
-orbitals. According to the
specified occupation (third line), the two ![]() -orbitals are occupied by
one electron each. The three
-orbitals are occupied by
one electron each. The three ![]()
![]() -orbitals are occupied uniformly
by
-orbitals are occupied uniformly
by ![]() of an electron each (0.6666 in lines 4, 5, and 6). Finally, the
of an electron each (0.6666 in lines 4, 5, and 6). Finally, the
![]()
![]() -orbital occupation is given by the last line. (See Example
-orbital occupation is given by the last line. (See Example
![[*]](crossref.png) on page
on page ![[*]](crossref.png) of the tutorial for the
discussion of the corresponding output).
of the tutorial for the
discussion of the corresponding output).
Because the Kohn-Sham method is a single-determinant approach, atomic states
are approximated by a single configuration (see however [164]
for a multi-determinantal approach). This can be done as in spatially
unrestricted Hartree-Fock calculations [165]. For ![]() and
and ![]() occupations, all possible configurations yield the correct spatial
symmetry. However, for
occupations, all possible configurations yield the correct spatial
symmetry. However, for ![]() occupations this is not the case and care
must be taken with the occupation scheme. Correct spatial symmetry
uniquely defines the orbital occupancies for
occupations this is not the case and care
must be taken with the occupation scheme. Correct spatial symmetry
uniquely defines the orbital occupancies for ![]() ,
, ![]() ,
, ![]() ,
,
![]() and
and ![]() . The other
. The other ![]() occupations are selected to maximize
the absolute angular momentum (this choice is arbitrary because
occupations are selected to maximize
the absolute angular momentum (this choice is arbitrary because ![]() is
no longer a good quantum number). Thus, the following
is
no longer a good quantum number). Thus, the following ![]() configurations must be used:
configurations must be used:
|
| : | |
|
| : |
|
|
| : |
|
|
| : |
|
|
| : |
|
|
| : |
|
|
| : |
|
|
| : |
|
|
| : |
|