next up previous contents
Next: Keyword LPCONSERVE Up: Born-Oppenheimer Molecular Dynamics Previous: Keyword TRAJECTORY   Contents


Keyword SIMULATION

This keyword controls property evaluations along BOMD trajectories.
Options:
ANALYZE / CALCULATE (must be specified)
ANALYZE A BOMD (property) calculation is analyzed.
CALCULATE A property calculation along a BOMD trajectory is requested.

DIPOLE / POLARIZABILITY / NMR / MAGNETIZABILITY MAGNETIZABILIIESA
DIPOLE Dipole moments are calculated along a BOMD trajectory.
POLARIZABILITY Polarizabilities are calculated along a BOMD trajectory.
NMR=$<$Integer$>$ NMR shieldings are calculated along a BOMD trajectory. The $<$Integer$>$ denotes the atom for which the magnetic shielding data are printed.
MAGNETIZABILITY Magnetizabilities are calculated along a BOMD trajectory.

MOMENTA / PHASESPACE
MOMENTA Linear and angular molecular momenta are calculated along an MD trajectory.
PHASESPACE The reduced coordinate and momentum are calculated along an MD trajectory. This option is valid only for dimers.

RDF / SIMILARITY / LINDEMANN / MEANDIS / PROLATE
RDF=A1-A2 Calculate the radial distribution function between atom A1 and atom A2.
SIMILARITY Calculate the similarity index along an MD trajectory with respect to pattern geometries.
LINDEMANN Calculate the Lindemann parameter for an MD trajectory.
MEANDIS Calculate the mean interatomic distance along an MD trajectory.
PROLATE Calculate the prolate deformation parameter along an MD trajectory.

LENGTH / ANGLE / DIHEDRAL
LENGTH Calculate the specified bond lengths along an MD trajectory.
ANGLE Calculate the specified angles along an MD trajectory.
DIHEDRAL Calculate the specified dihedral angles along an MD trajectory.

E=STANDARD / E=KINETIC / E=POTENTIAL / E=TOTAL / E=SYSTEM
E=STANDARD Standard output for the energy analysis of a trajectory file.
E=KINETIC The kinetic energy is averaged in the energy analysis of a trajectory file.
E=POTENTIAL The potential energy is averaged in the energy analysis of a trajectory file.
E=TOTAL The total energy is averaged in the energy analysis of a trajectory file.
E=SYSTEM The system energy is averaged in the energy analysis of a trajectory file.
INT=$<$Integer$>$ Step interval for property analysis or calculation. Default is 1.
Description:
In deMon2k, molecular dynamics property calculations proceed in two steps. First, a trajectory file, deMon.trj, is created by a BOMD run as described in 4.7.1. In the second step, properties are analyzed or calculated along the stored trajectory coordinates according to the options ANALYZE or CALCULATE of the keyword SIMULATION. It is important to note that the BOMD run and the property calculation are completely independent. Thus, different basis sets, functionals etc. can be used in the property calculation. When properties are calculated, the trajectory file deMon.trj is modified in order to store property values. Thus, it is important to note that the geometries and property data in the deMon.trj file are results of two independent calculations. Once the property values are stored in the trajectory file, they can be analyzed with the ANALYZE option. The SIMULATION options DIPOLE, POLARIZABILITY, NMR and MAGNETIZABILITY specify the property to be analyzed or calculated. A BOMD dipole calculation is triggered by the following input line: 

 SIMULATION CALCULATE DIPOLE

The corresponding output has the form: 

 TIME [FS] X[A.U.] Y[A.U.] Z[A.U.] |MU|[A.U.] <MU>[A.U.] <MU^2>[A.U]

    101.0   .089    .000    .835      .840       .840       .000
    102.0   .092    .000    .839      .844       .842       .002
    103.0   .093    .000    .842      .848       .844       .003
    104.0   .091    .000    .846      .851       .846       .004
    105.0   .088    .000    .850      .854       .847       .005
    106.0   .083    .000    .852      .856       .849       .006
    107.0   .076    .000    .855      .858       .850       .006
    108.0   .068    .000    .871      .874       .853       .010
    109.0   .060    .000    .864      .866       .855       .010
    110.0   .051    .000    .868      .870       .856       .010

For each time step, the instantaneous dipole moment components and the corresponding absolute dipole moment are listed, together with the average value and the standard deviation. The BOMD polarizability [33] output is similar and discussed in more detail in example [*] on page [*] of the tutorial.

A BOMD property calculation can be specified further by the corresponding property keyword. Note that NMR shieldings along BOMD trajectories are only printed for the atom specified by the NMR option of the SIMULATION keyword, even though all shieldings are calculated by default. To obtain the NMR shielding for a specific atom use SIMULATION ANALYZE NMR=$<$Integer$>$, where $<$Integer$>$ denotes the number of the desired atom in the GEOMETRY definition. The following input example, 

 TRAJECTORY RESTART PART=10-100 INT=1
 SIMULATION ANALYZE NMR=3 INT=1
 GEOMETRY CARTESIAN
 O    0.0000    0.0000    0.1173  17.0
 H    0.0000    0.7572   -0.4692 
 H    0.0000   -0.7572   -0.4692

generates an NMR shielding output for atom 3, here the second hydrogen of the water molecule, from trajectory step 10 to 100. Note the TRAJECTORY RESTART option that is used to address only a part of the trajectory file. Besides the detailed NMR shielding information (tensor diagonal elements, instantaneous shielding and averaged shielding) for the specified atom, the corresponding output lists also the NMR shielding statistics for all atoms. 

 **********************************************
 *** MOLECULAR DYNAMICS TRAJECTORY ANALYSIS ***
 **********************************************


                   NMR SHIELDING [ppm] FOR ATOM 3

 TIME [FS]      XX       YY       ZZ      SIGMA   <SIGMA>

     10.0      24.73    40.58    31.27    32.19    32.19
     11.0      24.01    39.42    29.88    31.11    31.65
     12.0      23.23    37.98    28.70    29.97    31.09
     13.0      22.70    36.99    28.05    29.25    30.63
     14.0      22.51    36.65    27.96    29.04    30.31
     15.0      22.70    37.04    28.41    29.38    30.16
     16.0      23.27    38.09    29.36    30.24    30.17
     17.0      24.03    39.36    30.52    31.31    30.31
     18.0      24.52    40.04    31.28    31.95    30.49
     19.0      24.36    39.48    31.18    31.68    30.61
     20.0      23.70    38.01    30.44    30.72    30.62
       :         :        :        :        :        :
     90.0      23.49    37.26    30.88    30.54    30.43
     91.0      23.05    36.30    30.36    29.90    30.43
     92.0      22.85    35.89    30.14    29.63    30.42
     93.0      22.94    36.10    30.29    29.78    30.41
     94.0      23.39    37.12    30.86    30.46    30.41
     95.0      24.27    39.07    31.74    31.69    30.42
     96.0      25.00    40.90    32.05    32.65    30.45
     97.0      24.71    40.92    30.93    32.19    30.47
     98.0      23.72    39.41    29.20    30.77    30.47
     99.0      23.02    38.12    28.13    29.76    30.46
    100.0      22.75    37.57    27.79    29.37    30.45

 *** NMR SHIELDINGS STATISTIC ***

 CHEMICAL SHIELDING FOR ATOM 1 ( O )
 AVERAGE SHIELDING [ppm] =   332.87
 STD DEV SHIELDING [ppm] =    13.06

 CHEMICAL SHIELDING FOR ATOM 2 ( H )
 AVERAGE SHIELDING [ppm] =    30.40
 STD DEV SHIELDING [ppm] =     0.81

 CHEMICAL SHIELDING FOR ATOM 3 ( H )
 AVERAGE SHIELDING [ppm] =    30.45
 STD DEV SHIELDING [ppm] =     1.02

The atoms for which NMR shieldings should be calculated along a BOMD trajectory can be selected with the READ option of the NMR keyword, see 4.8.8. Also the nuclear spin-rotation constant [226] can be calculated along BOMD trajectories as shown by the following input example. 

 DISPERSION
 BASIS (AUG-CC-PVDZ)
 AUXIS (GEN-A2)
 SCFTYPE MAX=1000 TOL=0.100E-04
 VXCTYPE OPTX-PBE AUXIS
 TRAJECTORY RESTART PART=10000-12000 INT=20
 SHIFT -0.2
 NMR SPINROT
 SIMULATION CALCULATE NMR=1 INT=20
 #
 # Cartesian coordinates of MD step 410000
 #
 GEOMETRY CARTESIAN ANGSTROM
 F   -66.916797   19.630729  -13.088069    9  18.998000
 H   -67.101518   18.720636  -12.997091    1   2.014000
 C    54.166066  -15.936748    9.958016    6  12.000000
 C    53.957601  -15.619981   11.173715    6  12.000000
 H    54.766661  -16.089846    9.024499    1   1.008000
 H    53.312450  -15.623649   12.049412    1   1.008000

Magnetizabilities [228] are calculated along a BOMD trajectory by the following input line: 

 SIMULATION CALCULATE MAGNETIZABILITY

Similarly to the spin-rotation constant, the rotational g-tensor [229] can be calculated along BOMD trajectories by specifying MAGNETIZABILITY GTENSOR in the the input.

The options MOMENTA and PHASESPACE are generic to MD simulations and, therefore, have no corresponding property keyword. While linear and angular momentum analyses are general, the PHASESPACE analysis can be performed only for diatomic molecules. In general, MOMENTA and PHASESPACE results probe the MD sampling in detail and are recommended if the calculation of thermodynamic properties from the MD trajectory is the objective. Plots from PHASESPACE outputs are shown in Figure 12.

The RDF, SIMILARITY, LINDEMANN, MEANDIS and PROLATE options are intended to be used in combination with the ANALYSE option to perform the respective analysis on an MD trajectory. The RDF option enables a radial distribution function calculation. It requires two string arguments to specify the atomic pair defining the radial distribution function. According to this specification the RDF for a specific atom pair or for all pairs of an element combination are calculated. Specific RDF options can be set by the RDF keyword (see 4.7.7) as in the following example. 

 RDF MAX=2.0 WIDTH=0.01
 SIMULATION ANALYSE RDF=C-H INT=10
 #
 GEOMETRY
 C        1.251600     -0.743355     -0.192056
 O        2.419080      0.016064      0.186570
 C       -0.012609      0.001665      0.300080
 H        3.194749     -0.353196     -0.223934
 O       -0.044331      1.355726     -0.228495
 H        0.628856      1.905515      0.161926
 C       -1.248651     -0.749384     -0.241064
 O       -2.455867     -0.060507      0.201783
 H       -2.338769      0.832194     -0.188720
 H       -0.073137     -0.089445      1.394002
 H       -1.226536     -1.787913      0.146590
 H        1.132009     -1.855775      0.371678
 H        1.127880     -0.963356     -1.265091
 H       -1.042307     -0.734311     -1.348578

This input generates an RDF for all C-H distances below 2 Ångström of a glycerol BOMD.

The SIMILARITY option requires the definition of at least one PATTERN geometry. This option triggers the calculation of the normalized RMS distance between the MD and PATTERN geometries which can be used as an index to classify isomers or calculate isomer lifetimes. By default, pattern and MD geometries are aligned (see 4.1.7) before anything is calculated. The automatic pattern-geometry alignment can be modified with the ALIGNMENT keyword if desired. The following input performs a similarity analysis, excluding hydrogen atoms, of glycerol conformers along a BOMD trajectory. 

 ALIGN ENANTIOMER EXCLUDE
 H
 SIMULATION ANALYSE SIMILARITY INT=1
 #
 # Pattern definitions
 #
 PATTERN GLYA
 C        0.000000      0.000000      0.000000
 O        0.000000      0.000000      1.462899
 C        1.474005      0.000000     -0.440301
 H       -0.893691     -0.260594      1.766994
 O        2.162480     -1.176562      0.084086
 H        1.941117     -1.214952      1.038194
 C        1.632514     -0.059827     -1.970356
 O        3.025324     -0.048486     -2.363928
 H        3.464920     -0.717132     -1.794492
 H        1.971460      0.922883     -0.056060
 H        1.170832      0.835048     -2.435026
 H       -0.510825      0.910396     -0.391119
 H       -0.502224     -0.913371     -0.392432
 H        1.121602     -0.977513     -2.350343
 PATTERN GLYB
 C        0.000000      0.000000      0.000000
 O        0.000000      0.000000      1.447257
 C        1.448191      0.000000     -0.553309
 H        0.683368      0.660325      1.699576
 O        2.197151      1.114528      0.025822
 H        1.975852      1.886268     -0.546110
 C        1.505454      0.056976     -2.092055
 O        1.020939      1.380454     -2.494249
 H        1.337270      1.554323     -3.403051
 H       -0.524157     -0.927069     -0.313648
 H        2.557147     -0.088302     -2.425107
 H        0.859665     -0.741313     -2.524473
 H       -0.548895      0.882612     -0.405640
 H        1.966016     -0.916375     -0.200050
 GEOMETRY
 C        1.251600     -0.743355     -0.192056
 C        2.419080      0.016064      0.186570
 C       -0.012609      0.001665      0.300080
 O        3.194749     -0.353196     -0.223934
 O       -0.044331      1.355726     -0.228495
 O        0.628856      1.905515      0.161926
 H       -1.248651     -0.749384     -0.241064
 H       -2.455867     -0.060507      0.201783
 H       -2.338769      0.832194     -0.188720
 H       -0.073137     -0.089445      1.394002
 H       -1.226536     -1.787913      0.146590
 H        1.132009     -1.855775      0.371678
 H        1.127880     -0.963356     -1.265091
 H       -1.042307     -0.734311     -1.348578

With the Lindemann option the root-mean-square bond length fluctuation [230], @fnswfnvalfnswfalse ##1fnval##1fnswtrue

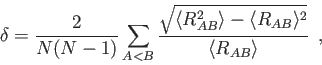\begin{displaymath} \delta = {2 \over {N (N - 1)}} \sum_{A<B} {\sqrt{\langle ... ...gle R_{AB} \rangle^2} \over \langle R_{AB} \rangle } \> \>,% \end{displaymath} (19)

with $N$ and $R_{AB}$ being the number of atoms and interatomic distances, respectively, are calculated along a trajectory. Similarly, the mean interatomic distance [231], @fnswfnvalfnswfalse ##1fnval##1fnswtrue
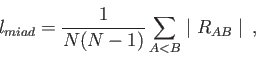\begin{displaymath} l_{miad} = {1 \over {N (N - 1)}} \sum_{A<B} \mid R_{AB} \mid \> \>,% \end{displaymath} (20)

is calculated with the MEANDIS option. It measures the average "extension" of a structure in a molecular dynamics simulation. The prolate deformation coefficient [232], @fnswfnvalfnswfalse ##1fnval##1fnswtrue
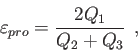\begin{displaymath} \varepsilon_{pro} = {2 Q_1 \over {Q_2 + Q_3}} \> \>,% \end{displaymath} (21)

with $Q_1 \ge Q_2 \ge Q_3$ being the eigenvalues of the geometrical quadrupole tensor over all atoms with elements, @fnswfnvalfnswfalse ##1fnval##1fnswtrue
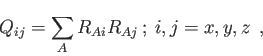\begin{displaymath} Q_{ij} = \sum_A R_{Ai} R_{Aj} \> ; \> i,j = x,y,z \> \>,% \end{displaymath} (22)

are calculated along a trajectory with the PROLATE option.

The LENGTH, ANGLE and DIHEDRAL options require the definition of the atoms involved, in the next input lines. Two numbers are required to define each bond LENGTH, three numbers to define each ANGLE and four numbers to define each DIHEDRAL angle. Up to ten parameters can be defined in this way, in consecutive lines after the keyword, as the following input example shows. 

 SIMULATION ANALYSE DIHEDRAL INT=10
 2 1 3 7
 2 1 3 5
 8 7 3 1
 8 7 3 5
 1 5 3 8
 8 3 5 1
 4 5 6 7
 7 6 5 4
 3 1 10 2
 12 11 10 9
 #
 GEOMETRY
 C        1.251600     -0.743355     -0.192056
 O        2.419080      0.016064      0.186570
 C       -0.012609      0.001665      0.300080
 H        3.194749     -0.353196     -0.223934
 O       -0.044331      1.355726     -0.228495
 H        0.628856      1.905515      0.161926
 C       -1.248651     -0.749384     -0.241064
 O       -2.455867     -0.060507      0.201783
 H       -2.338769      0.832194     -0.188720
 H       -0.073137     -0.089445      1.394002
 H       -1.226536     -1.787913      0.146590
 H        1.132009     -1.855775      0.371678
 H        1.127880     -0.963356     -1.265091
 H       -1.042307     -0.734311     -1.348578

The standard energy output of a deMon BOMD run has the following form: 

 TIME [FS]  T [K]   EKIN        EPOT        ETOT     <T> [K]   <ETOT> 

     10.0   103.5   0.00098  -648.62892  -648.62793   103.0  -648.62793
     20.0   100.3   0.00095  -648.62889  -648.62794   102.7  -648.62793
     30.0    91.4   0.00087  -648.62885  -648.62799   100.2  -648.62795
     40.0    84.9   0.00081  -648.62882  -648.62801    96.8  -648.62796
     50.0    84.2   0.00080  -648.62874  -648.62794    94.2  -648.62797
     60.0   107.4   0.00102  -648.62869  -648.62767    94.3  -648.62794
     70.0   185.8   0.00176  -648.62858  -648.62681   102.2  -648.62784
     80.0   252.2   0.00240  -648.62831  -648.62592   118.8  -648.62763
     90.0   154.0   0.00146  -648.62799  -648.62653   128.2  -648.62747
    100.0    56.3   0.00053  -648.62772  -648.62719   124.2  -648.62742

For each time step it lists the instantaneous temperature, kinetic, potential, and total energy as well as the average temperature and total energy. With the INT option of the SIMULATION keyword, the step interval for the energy output can be modified. Energy statistics along an existing trajectory file can be obtained with: 

 SIMULATION ANALYZE E=STANDARD

If E=STANDARD is substituted by E=KINETIC, E=POTENTIAL, E=TOTAL, or E=SYSTEM, the averages of the kinetic, potential, total or system2 energies are listed. In the case of E=KINETIC the output takes the form: 

 TIME [FS]  EKIN        EPOT        ESYS        ETOT         <EKIN> 

     10.0   0.00098  -648.62892  -648.62793  -648.62793     0.0009836
     20.0   0.00095  -648.62889  -648.62791  -648.62794     0.0009680
     30.0   0.00087  -648.62885  -648.62795  -648.62799     0.0009348
     40.0   0.00081  -648.62882  -648.62798  -648.62801     0.0009027
     50.0   0.00080  -648.62874  -648.62788  -648.62794     0.0008821
     60.0   0.00102  -648.62869  -648.62765  -648.62767     0.0009051
     70.0   0.00176  -648.62858  -648.62747  -648.62681     0.0010279
     80.0   0.00240  -648.62831  -648.62741  -648.62592     0.0011989
     90.0   0.00146  -648.62799  -648.62729  -648.62653     0.0012282
    100.0   0.00053  -648.62772  -648.62710  -648.62719     0.0011588

After the trajectory output, energy and temperature statistics are printed. As for the DYNAMICS keyword, the SIMULATION keyword can be combined with the TRAJECTORY keyword in order to analyze or calculate properties for parts of a trajectory.

Footnotes

... system2
The system energy refers to the extended system energy of the Nosé type thermostats.
next up previous contents
Next: Keyword LPCONSERVE Up: Born-Oppenheimer Molecular Dynamics Previous: Keyword TRAJECTORY   Contents