Keyword POLARIZABILITY

This keyword activates the calculation of polarizabilities.
Options:
ALPHA / BETA / GAMMA

	ALPHA		The polarizability tensor ${\mbox{\boldmath$\alpha$}}$ is calculated.This is the default.
	BETA		The first hyperpolarizability $\beta$ is calculated.
	GAMMA		The second hyperpolarizability $\gamma$ is calculated.

ANALYTICAL / NIACPKS / NUMERICAL

	ANALYTICAL		The polarizability is calculated analytically. This is the default.
	NIACPKS		The polarizability is calculated with the non-iterative coupled-perturbed Kohn-Sham method.
	NUMERICAL		The polarizability is calculated numerically with a finite-field method.

DD / DQ

	DD		Dipole-dipole polarizabilities are calculated. This is the default.
	DQ		Dipole-quadrupole polarizabilities are calculated. Only valid in combination with the option ANALYTICAL.

SHG / EOPE / OR

	SHG		Calculate second harmonic generation. Only valid in combination with the options ANALYTICAL and W=Real.
	EOPE		Calculate electro-optical Pockels effect. Only valid in combination with the options ANALYTICAL and W=Real.
	OR		Calculate optical rectification. Only valid in combination with the options ANALYTICAL and W=Real.

	W=Real		Dynamical polarizability frequency (or wavelength) that can be given in a.u., eV, cm $^{-1}$ , and nm by the unit abbreviations AU, EV, CM, and NM, respectively. By default, the field frequency is given in atomic units. The form W1=Real is an equivalent input format.
	W2=Real		Second dynamical hyperpolarizability frequency. Input format as for W=Real.
	EFISH		Activate the EFISH orientation.

	FFS=Real		Finite field strength for the polarizability calculation with the option NUMERICAL.
	TOL=Real		Threshold for numerical exchange-correlation kernel derivative pruning. Default value is 1.0.
	FALDA		The LDA kernel will be used in the response equation system. Note that this setting will apply to all response calculations in a run.
	GALDA		The LDA kernel derivative will be used for the hyperpolarizability response equation system.
	FDKERNEL		A finite difference kernel will be used in the response equation system. Note that this setting will apply to all response calculations in a run.

Description:
In deMon2k polarizabilities can be calculated either analytically by auxiliary density perturbation theory (ADPT) [30,158], semi-numerically by the non-iterative coupled-perturbed Kohn-Sham (NIA-CPKS) method [37] or numerically by the finite-field method [36]. The method is selected with the options ANALYTICAL, NIACPKS or NUMERICAL. All three methods are available for RKS, UKS and ROKS. The mean polarizability $\overline{\alpha}$ and polarizability anisotropy ${\vert \Delta \alpha \vert}^2$ are calculated in the principal axis system of the polarizability tensor as:

$\displaystyle \overline{\alpha}$	$\textstyle =$	$\displaystyle {1 \over 3} \left ( {\alpha}_{xx} + {\alpha}_{yy} + {\alpha}_{zz} \right )$	(23)
$\displaystyle {\vert \Delta \alpha \vert}^2$	$\textstyle =$	$\displaystyle {1 \over 2} \left [ ( {\alpha}_{xx} - {\alpha}_{yy} )^2 + ( {\alpha}_{xx} - {\alpha}_{zz} )^2 + ( {\alpha}_{yy} - {\alpha}_{zz} )^2 \right ]$	(24)

Dipole-quadrupole polarizabilities [242] can be calculated with the option ANALYTICAL or NIACPKS employing the DQ option of the POLARIZABILITY keyword. First hyperpolarizabilites, $\beta$ can be calculated with the options ANALYTICAL or NUMERICAL specifying BETA in the POLARIZABILITY keyword line.


 DIPOLES
 GRID FINE
 SYMMETRY ON
 AUXIS (GEN-A2*)
 BASIS (TZVP-FIP1)
 VXCTYP AUXIS BLYP
 POLARIZABILITY BETA ANALYTICAL EFISH
 #
 Geometry Z-Matrix
 C1
 O1   C1   LCO1
 Constants
 LCO1   1.1281

In analytic first hyperpolarizability calculations the full $\beta$ tensor is calculated as the following output shows.


 MOLECULE ORIENTATION FOR POLARIZABILITIES IN ANGSTROM

  NO.  ATOM     X           Y           Z        Z-ATOM   MASS   TYPE

    1  C1     0.000000    0.000000   -0.644365       6    12.011  QM
    2  O1     0.000000    0.000000    0.483735       8    15.999  QM


 *** HYPERPOLARIZABILITY ***


 BETA TENSOR COMPONENTS XIJ

                 1             2             3
     1        0.118052      0.097283      5.999359
     2        0.097283      0.004124     -0.040942
     3        5.999359     -0.040942     -0.133288


 BETA TENSOR COMPONENTS YIJ

                 1             2             3
     1        0.097283      0.004124     -0.040942
     2        0.004124     -0.053564      5.749705
     3       -0.040942      5.749705     -0.182612


 BETA TENSOR COMPONENTS ZIJ

                 1             2             3
     1        5.999359     -0.040942     -0.133288
     2       -0.040942      5.749705     -0.182612
     3       -0.133288     -0.182612     26.180178


 HYPERPOLARIZABILITY TENSOR NORMS [A.U.]

 DIPOLAR BETA NORM     :      29.38
 QUADRUPOLAR BETA NORM :       5.44
 TOTAL BETA TENSOR NORM:      29.88

 AVERAGE FIRST HYPERPOLARIZABILITY:      22.76

In numerical first hyperpolarizabilty calculations only selected components of the $\beta$ tensor are calculated. Therefore, the numerical $\beta$ calculations are always performed in the so-called EFISH (Electric Field Induced Second Harmonic generation) orientation. In it, the -axis of the molecule is oriented along the permanent dipole moment of the system. The same holds for numerical second hyperpolarizability, $\gamma$ , calculations. In EFISH orientation, the mean first and second hyperpolarizabilities are defined as:

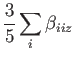$\displaystyle \overline{\beta}$	$\textstyle =$	$\displaystyle {3 \over 5} \sum_i {\beta}_{iiz}$	(25)
$\displaystyle \overline{\gamma}$	$\textstyle =$	$\displaystyle {1 \over 5} \sum_{i,j} {\gamma}_{iijj}$	(26)

Thus, the AVERAGE FIRST HYPERPOLARIZABILTY of a numerical $\beta$ calculation,


 MOLECULE ORIENTATION FOR POLARIZABILITIES IN ANGSTROM

  NO.  ATOM     X           Y           Z        Z-ATOM   MASS   TYPE

    1  C1     0.000000    0.000000   -0.644365       6    12.011  QM
    2  O1     0.000000    0.000000    0.483735       8    15.999  QM


 *** FIRST HYPERPOLARIZABILITY ***

 INDUCED DIPOLE MOMENTS (IN A.U.)

 ELECTRIC FIELD                X          Y          Z      SCF CYCLES
 ---------------------------------------------------------------------
 Fz(-0.0100)                0.000000  -0.000000  -0.087547      12
 Fz(-0.0100)  Fz(-0.0100)   0.000000   0.000000  -0.244794      13
 Fy(-0.0100)                0.000000  -0.123112   0.070726      14
 Fy(-0.0100)  Fy(-0.0100)  -0.000000  -0.247706   0.071423      15
 Fx(-0.0100)               -0.123112  -0.000000   0.070726      14
 Fx(-0.0100)  Fx(-0.0100)  -0.247706  -0.000000   0.071423      15
 Fx(+0.0100)                0.123112   0.000000   0.070726      14
 Fx(+0.0100)  Fx(+0.0100)   0.247706  -0.000000   0.071423      15
 Fy(+0.0100)               -0.000000   0.123112   0.070726      14
 Fy(+0.0100)  Fy(+0.0100)  -0.000000   0.247706   0.071423      15
 Fz(+0.0100)                0.000000   0.000000   0.230419      11
 Fz(+0.0100)  Fz(+0.0100)   0.000000   0.000000   0.395391      12


 FIRST HYPERPOLARIZABILITY [A.U.]

 BETA(XXX) =  0.00021   BETA(XYY) = -0.00000   BETA(XZZ) =  0.00000
 BETA(YXX) =  0.00000   BETA(YYY) = -0.00000   BETA(YZZ) =  0.00000
 BETA(ZXX) =  4.64573   BETA(ZYY) =  4.64570   BETA(ZZZ) = 25.74926


 AVERAGE FIRST HYPERPOLARIZABILITY:      21.02

always refers to the EFISH orientation. As a consequence, analytical and numerical $\bar \beta$ results can only be directly compared by using this orientation in both calculations!

Dynamical polarizabilities [243] and hyperpolarizabilities [244] can only be calculated with the analytical ADPT approach, i.e. with the option ANALYTICAL. In these calculations the option W=Real (or its alternative form W1=Real) specifies the frequency (or wavelength) of the (first) external field. It can be given in a.u., eV, cm $^{-1}$ , or nm by using the corresponding unit abbreviation. By default W is set to zero. Note that for polarizabilities imaginary frequencies are also possible [245]. They are defined in the input by real numbers with a leading i, i.e.

 POLARIZABILITY ALPHA W = i4.7257

If for dynamical first hyperpolarizabilities only one frequency is specified either the second harmonic generation (SHG), the electro-optical Pockels effect (EOPE) or the optical rectification (OR) is calculated. These non-linear optical properties are characterized by the following frequency combinations for the dynamical $\beta$ tensor elements $\beta_{xyz}(-\omega_3;\omega_1,\omega2)$ [246]:

SHG	$\omega_1$	=	$\pm \omega$	$\omega_2$	=	$\pm \omega$	$\omega_3$	=	$\pm 2 \omega$
EOPE	$\omega_1$	=		$\omega_2$	=	$\pm \omega$	$\omega_3$	=	$\pm \omega$
OR	$\omega_1$	=	$\pm \omega$	$\omega_2$	=	$\mp \omega$	$\omega_3$	=

By default the SHG is calculated as with the following input line.

 POLARIZABILITY BETA ANALYTICAL EFISH W=0.199 au

To calculate the EOPE use:

 POLARIZABILITY BETA ANALYTICAL EFISH W=0.199 au EOPE

With the W2=Real option a second frequency for dynamical $\beta$ calculations can be explicitly specified in the input.

The default finite-field strength for the numerical polarizability calculations is 0.01 atomic units. With the option FFS, that field strength can be modified. Please note that the calculated polarizabilities are sensitive to both the finite field strength and the SCF convergence. With the FALDA and GALDA options the use of the LDA kernel and kernel derivative is requested, respectively, independent of the functional specified with the VXCTYPE keyword (see 4.2.1). With the FDKERNEL option a finite-difference kernel calculation [37] is requested. This permits static and dynamic ADPT polarizability calculations for all LDA and GGA functionals for which a potential is implemented. By default the FDKERNEL option is only activated for functionals for which no analytic ADPT kernel is available [247]. Note that the FALDA, GALDA and FDKERNEL settings apply to all response calculations in a deMon2k run.