Next: Keyword FORCEFIELD Up: Methodology Selection Previous: Keyword VXCTYPE Contents
| ON | An empirical dispersion term is added. | ||
| OFF | No empirical dispersion term is added. | ||
| READ | The C | ||
|
S6= | Global scaling factor. The default value is 1.0. |
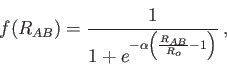 |
(3) |
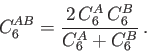 |
(4) |
DISPERSION READ F1 10.74
Here the ![]() dispersion coefficient must be given in atomic units.
Atoms for which
dispersion coefficient must be given in atomic units.
Atoms for which ![]() coefficients are set to zero do not contribute to the
deMon2k dispersion energy.
coefficients are set to zero do not contribute to the
deMon2k dispersion energy.