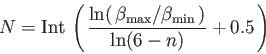Automatic Generation of Auxiliary Functions
Automatically generated auxiliary function sets are provided in deMon2k
by means of the auxiliary function specification GEN-A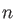 , with
, with 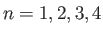 , and
GEN-A
, and
GEN-A *, with
*, with 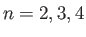 [133,156]. The GEN-A1 set possesses
only
[133,156]. The GEN-A1 set possesses
only 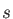 auxiliary functions and is usually used only for debugging. The
GEN-A
auxiliary functions and is usually used only for debugging. The
GEN-A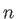 sets consist of
sets consist of 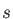 ,
, 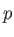 , and
, and 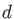 Hermite Gaussian functions. In
addition, the GEN-A
Hermite Gaussian functions. In
addition, the GEN-A * also have
* also have 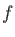 and
and 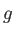 Hermite Gaussians. Because the
auxiliary functions are used to fit the electron density they are grouped
in
Hermite Gaussians. Because the
auxiliary functions are used to fit the electron density they are grouped
in 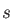 ,
, 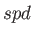 , and
, and 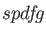 sets. The exponents are shared within each of
these sets [53,54]. Therefore, the auxiliary function notation
(3,2,2) describes 3
sets. The exponents are shared within each of
these sets [53,54]. Therefore, the auxiliary function notation
(3,2,2) describes 3 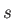 sets with a total of 3 functions, 2
sets with a total of 3 functions, 2  sets
with a total of 20 functions and 2
sets
with a total of 20 functions and 2 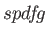 sets with a total of 70
functions (see also 4.3.3). The range of exponents of all automatically
generated auxiliary functions is determined by the smallest,
sets with a total of 70
functions (see also 4.3.3). The range of exponents of all automatically
generated auxiliary functions is determined by the smallest,
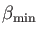 ,
and largest,
,
and largest,
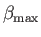 , primitive Gaussian exponent of the specified
orbital basis set. Therefore, the GEN-A
, primitive Gaussian exponent of the specified
orbital basis set. Therefore, the GEN-A and GEN-A
and GEN-A * auxiliary function
sets differ for different orbital basis sets. The number of exponents
* auxiliary function
sets differ for different orbital basis sets. The number of exponents
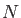 (auxiliary function sets) is given by:
(auxiliary function sets) is given by:
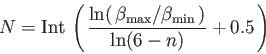 |
(1) |
Here 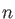 is 1, 2, 3, or 4 according to the index of the selected GEN-A
is 1, 2, 3, or 4 according to the index of the selected GEN-A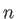 or GEN-A
or GEN-A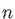 * set. The exponents are generated in almost even-tempered form
(see details below) and split into
* set. The exponents are generated in almost even-tempered form
(see details below) and split into 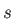 ,
, 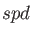 and, if a GEN-A
and, if a GEN-A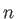 * set is
specified,
* set is
specified, 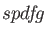 sets. The tightest (largest) exponents are assigned
to the
sets. The tightest (largest) exponents are assigned
to the 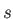 sets, followed by the
sets, followed by the 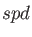 , and, if specified,
, and, if specified,  sets.
The basic exponent from which the generation starts is defined as:
sets.
The basic exponent from which the generation starts is defined as:
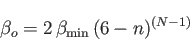 |
(2) |
In case ECPs or MCPs are used, equation (A..2) changes to:
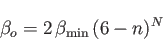 |
(3) |
Furthermore, only  and
and 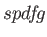 sets are generated on ECP and MCP
centers. From
sets are generated on ECP and MCP
centers. From 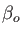 the two tightest
the two tightest 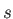 , or
, or 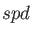 set exponents,
set exponents,
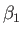 and
and  are generated according to the formulas:
are generated according to the formulas:
The other 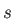 or
or 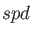 set exponents are generated according to the
even-tempered progression:
set exponents are generated according to the
even-tempered progression:
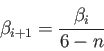 |
(6) |
The 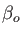 exponent of the subsequent
exponent of the subsequent 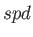 sets is also generated according
to the progression (A..6). Based on this
sets is also generated according
to the progression (A..6). Based on this 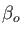 exponent, the
exponents of the first two
exponent, the
exponents of the first two 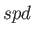 sets are calculated with the formulas
(A..4) and (A..5). The subsequent
sets are calculated with the formulas
(A..4) and (A..5). The subsequent 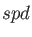 set exponents are calculated again according to the even-tempered
progression (A..6). In the same way, the
set exponents are calculated again according to the even-tempered
progression (A..6). In the same way, the 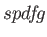 set exponents
are calculated. In the case of
set exponents
are calculated. In the case of 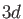 elements, an extra diffuse
elements, an extra diffuse  auxiliary
function set is added.
auxiliary
function set is added.