Next: Keyword DOS Up: Electronic Structure Analysis Previous: Electronic Structure Analysis Contents
| MULLIKEN | A Mulliken population analysis is performed. This is the default. | ||
| LOEWDIN | A Löwdin population analysis is performed. | ||
| BADER | A Bader population analysis is performed. | ||
| NBO | Create input file for an NBO analysis. | ||
| BECKE | Real space is partitioned into overlapping (fuzzy) Becke cells. | ||
| HIRSHFELD | Real space is partitioned into overlapping Hirshfeld cells. | ||
| VORONOI | Real space is partitioned into non-overlapping Voronoi cells. |
| SCF | The SCF density is used for the Hirshfeld weights. Only meaningful for the HIRSHFELD option. | ||
| ITERATIVE | The Hirshfeld weights are refined iteratively. Only meaningful for the HIRSHFELD option. | ||
| FRACTIONAL | Same as the ITERATIVE option but separates | ||
| DEFORMATION | The deformation density is analyzed. Only meaningful for the BECKE, HIRSHFELD and VORONOI options. | ||
| FULL | More information is printed. |
With the options BECKE, HIRSHFELD or VORONOI a topological atom-in-molecule (AIM)
analysis of the electronic density is performed. The electronic density,
![]() is integrated numerically on a fixed grid of points. By selecting the BASIS or AUXIS
option of the TOPOLOGY keyword (see 4.10.2), the user triggers the analysis
of the Kohn-Sham density (BASIS) or of the auxiliary density (AUXIS). By default the
Kohn-Sham density is used for all topological analyses. The quality of the integration
grid is also set with the TOPOLOGY keyword using the options COARSE, MEDIUM, FINE or
REFERENCE. The DEFORMATION option of the POPULATION keyword triggers the analysis of
the deformation density,
is integrated numerically on a fixed grid of points. By selecting the BASIS or AUXIS
option of the TOPOLOGY keyword (see 4.10.2), the user triggers the analysis
of the Kohn-Sham density (BASIS) or of the auxiliary density (AUXIS). By default the
Kohn-Sham density is used for all topological analyses. The quality of the integration
grid is also set with the TOPOLOGY keyword using the options COARSE, MEDIUM, FINE or
REFERENCE. The DEFORMATION option of the POPULATION keyword triggers the analysis of
the deformation density,
![]() , defined as:
, defined as:
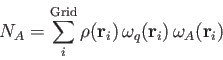 |
(38) |
Voronoi:
 |
(39) |
Becke:
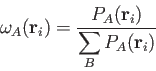 |
(40) |
Hirshfeld:
The cell function
![]() of the BECKE weights is defined by a "soft" step
function in terms of the elliptic coordinates
of the BECKE weights is defined by a "soft" step
function in terms of the elliptic coordinates ![]() defined as [269]:
defined as [269]:
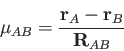 |
(42) |
As can be seen from Eq. (4.32) the atomic Hirshfeld weights are always
calculated from the auxiliary densities, independent of whether the Kohn-Sham or
auxiliary density is partitioned. For the reference densities in Eq. (4.32)
4 different options are available. By default spherically averaged neutral atom
densities are used to calculate the atomic Hirshfeld weights. This is the standard
Hirshfeld scheme from the literature [265]. With the SCF option of the
POPULATION keyword ![]() is calculated from the atomic SCF auxiliary densities.
With the ITERATIVE option
is calculated from the atomic SCF auxiliary densities.
With the ITERATIVE option ![]() of each atom is calculated from a spherically
averaged ion with the current charge of the atom (see Eq. 19 of Ref. [266]).
Note that this approach is computationally more involved than the standard Hirshfeld
scheme because it requires repetitive integration of the electronic density over the
grid. The tolerance criteria and the maximum number of iterations are set by the
TOPOLOGY keyword options TOL and MAX, respectively. The iterative Hirshfeld scheme
produces higher partial charges in absolute value than the standard one and is also
applicable to ionic molecules. Moreover the arbitrariness in the definition of the
reference densities of the standard Hirshfeld approach is removed with the iterative
version. In open-shell molecules either the density or the spin densities can be
refined iteratively according to scheme that was just discussed. This selection is
triggered by the options ITERATIVE or FRACTIONAL, respectively. Therefore, the input
lines,
of each atom is calculated from a spherically
averaged ion with the current charge of the atom (see Eq. 19 of Ref. [266]).
Note that this approach is computationally more involved than the standard Hirshfeld
scheme because it requires repetitive integration of the electronic density over the
grid. The tolerance criteria and the maximum number of iterations are set by the
TOPOLOGY keyword options TOL and MAX, respectively. The iterative Hirshfeld scheme
produces higher partial charges in absolute value than the standard one and is also
applicable to ionic molecules. Moreover the arbitrariness in the definition of the
reference densities of the standard Hirshfeld approach is removed with the iterative
version. In open-shell molecules either the density or the spin densities can be
refined iteratively according to scheme that was just discussed. This selection is
triggered by the options ITERATIVE or FRACTIONAL, respectively. Therefore, the input
lines,
POPULATION HIRSHFELD ITERATIVE
and
POPULATION HIRSHFELD FRACTIONAL
yield the same iterative Hirshfeld charges for closed-shell molecules but different charges for open-shell molecules.